フォワードプロパゲーションについて解説

フォワードプロパゲーション（順伝播処理）とは、ニューラルネットワークにおいてネットワークを入力層から出力層にデータを流す過程のことで、入力データを順方向に伝搬させ出力値を計算します。

目次

1. フォワードプロパゲーションの流れ
2. 入力層
   1. 入力層の入力・出力
3. 隠れ層
   1. 隠れ層の入力
      1. 隠れ層の重み行列
   2. 隠れ層の総入力
   3. 隠れ層の出力
      1. 隠れ層の活性化関数
         1. シグモイド関数
4. 出力層
   1. 出力層の入力
      1. 出力層の重み行列
   2. 出力層の総入力
   3. 出力層の出力
      1. 出力層の活性化関数
5. フォワードプロパゲーションをPythonで実装する

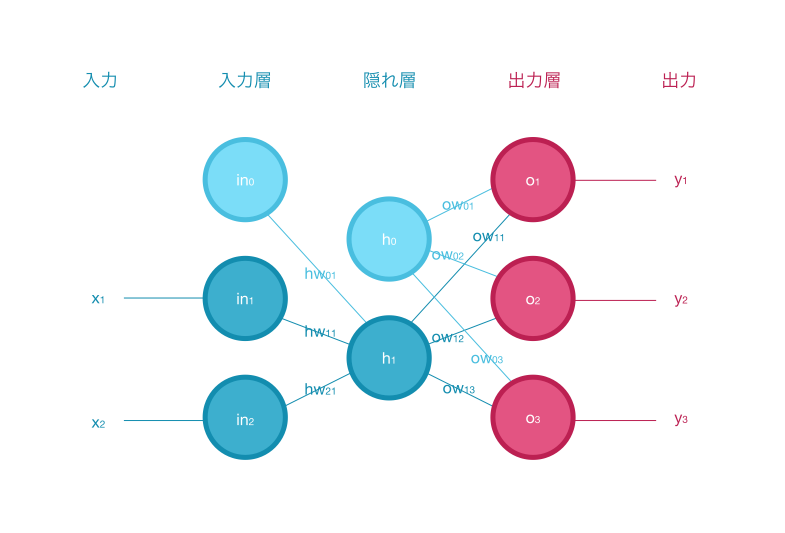
フォワードプロパゲーションの流れ

フォワードプロパゲーションでは、下記の流れで入力データを順方向に伝搬させ出力値を計算します。

1. 入力層
   1. 入力層の入力・出力：入力データのベクトルを出力
2. 隠れ層
   1. 隠れ層の入力：入力層の出力と隠れ層の重みの積を入力
   2. 隠れ層の総入力：隠れ層の入力にバイアスを足す
   3. 隠れ層の出力：隠れ層の総入力を活性化関数に渡して出力
3. 出力層
   1. 出力層の入力：隠れ層の出力と出力層の重みの積を入力
   2. 出力層の総入力：出力層の入力にバイアスを足す
   3. 出力層の出力：出力層の総入力を活性化関数に渡して出力

入力層

入力層の入力・出力

入力データのベクトルを入力層の入力として作成します。

入力層のユニット数は入力データ数+バイアスとなります。

バイアスとは、1を出力する度合いを調整するための値（出力の閾値）のことです。

$$
input\_layer\_output =
\begin{bmatrix}
in_0 \,
in_1 \,
… \,
in_i \,
\end{bmatrix} \\
\hspace{70pt} =
\begin{bmatrix}
b \,
x_1 \,
… \,
x_i \,
\end{bmatrix}
$$

上記のベクトルを入力層の出力として出力します。

# 入力層のユニット数
input_layer_units = 9
# ベクトル
input_layer_output = np.random.randn(input_layer_units)

# ベクトルの形状
input_layer_output.shape

(9,) # 入力データ数+バイアス

隠れ層

隠れ層の入力

入力層の出力と隠れ層の重みの積を隠れ層の入力とします。
$$
hidden\_layer\_inputs =
\begin{bmatrix}
in_0 \, in_1 \, … \, in_i \,
\end{bmatrix}
\begin{bmatrix}
hw_{01} \, hw_{02} \, … \, hw_{0h} \\
hw_{11} \, hw_{12} \, … \, hw_{1h} \\
… \\
hw_{i1} \, hw_{i2} \, … \, hw_{ih} \\
\end{bmatrix} \\
\hspace{-5pt} =
\begin{bmatrix}
hi_0 \, hi_1 \, … \, hi_h \,
\end{bmatrix}
$$

隠れ層の重み行列

隠れ層の重み行列は、行数は入力層のユニット数、列数は隠れ層のユニット数となります。

$$
hidden\_layer\_weights =
\begin{bmatrix}
hw_{01} \, hw_{02} \, … \, hw_{0h} \\
hw_{11} \, hw_{12} \, … \, hw_{1h} \\
… \\
hw_{i1} \, hw_{i2} \, … \, hw_{ih} \\
\end{bmatrix}
$$

# 隠れ層のユニット数
hidden_layer_units = 7
# 隠れ層の重み行列
hidden_layer_weights = np.random.randn(input_layer_units, hidden_layer_units)

# 重み行列の形状
hidden_layer_weights.shape

(9, 7) # 入力層のユニット数×隠れ層のユニット数

隠れ層の総入力

隠れ層の総入力は、隠れ層の入力にバイアスを足したものとなります。

隠れ層の出力

隠れ層の総入力を活性化関数に渡して、隠れ層の出力として出力します。

隠れ層の活性化関数

活性化関数とは、入力値を別の数値に変換して出力し、モデルの表現力を上げる関数のことです。

シグモイド関数を活性化関数として使い、隠れ層の出力とします。

$$
hidden\_layer\_output = sigmoid(hidden\_layer\_total\_input)
$$

シグモイド関数

シグモイド関数は、入力値を0.0〜1.0の範囲の数値に変換して出力する関数です。

重みを学習するには微分可能にする必要があるため、非線形の活性化関数であるシグモイド関数を使用します。

$$
sigmoid=\frac{1}{1+e^{-z}}
$$

出力層

出力層の入力

隠れ層の出力と出力層の重みの積を出力層の入力とします。

$$
output\_layer\_inputs =
\begin{bmatrix}
ho_0 \, ho_1 \, … \, ho_i \,
\end{bmatrix}
\begin{bmatrix}
ow_{01} \, ow_{02} \, … \, ow_{0o} \\
ow_{11} \, ow_{12} \, … \, ow_{1o} \\
… \\
ow_{h1} \, ow_{h2} \, … \, ow_{ho} \\
\end{bmatrix} \\
\hspace{-8pt} =
\begin{bmatrix}
oi_0 \, oi_1 \, … \, oi_o
\end{bmatrix}
$$

出力層の重み行列

出力層の重み行列は、行数は隠れ層のユニット数、列数は出力層のユニット数となります。

$$
output\_layer\_weights =
\begin{bmatrix}
ow_{01} \, ow_{02} \, … \, ow_{0o} \\
ow_{11} \, ow_{12} \, … \, ow_{1o} \\
… \\
ow_{h1} \, ow_{h2} \, … \, ow_{ho} \\
\end{bmatrix}
$$

# 出力層のユニット数
output_layer_units = 8
# 出力層の重み行列
output_layer_weights = np.random.randn(hidden_layer_units, output_layer_units)

# 重み行列の形状
output_layer_weights.shape

(7, 8) # 隠れ層のユニット数×出力層のユニット数

出力層の総入力

出力層の総入力は、出力層の入力にバイアスを足したものとなります。

出力層の出力

出力層の総入力を活性化関数に渡して、出力層の出力として出力します。

出力層の活性化関数

隠れ層と同様に、シグモイド関数を活性化関数として使い、出力層の出力とします。

$$
output\_layer\_output = sigmoid(output\_layer\_total\_input)
$$

フォワードプロパゲーションをPythonで実装する

上記のフォワードプロパゲーションの流れをPythonで実装します。

フォワードプロパゲーションの一連の処理は、関数にまとめて実装しています。

import numpy as np
import math

### 活性化関数
## シグモイド関数
def sigmoid(input):
    return 1 / (1 + math.e**-input)

# 乱数シードを固定
np.random.seed(seed=42)

### 入力層
## 入力層の入力・出力
# 入力層のユニット数
input_layer_units = 9
# ベクトル
input_layer_output = np.random.randn(input_layer_units)

def forward_propagation(units, previous_layer_units, previous_layer_output):
    ## 引数
    # units：層のユニット数
    # previous_layer_units：前の層のユニット数
    # previous_layer_output：前の層の出力

    ## 層の入力
    # 層のバイアス
    bias = np.random.randn(units)
    # 層の重み行列
    weights = np.random.randn(previous_layer_units, units)
    # 層の入力
    inputs = np.dot(previous_layer_output, weights)
    ## 層の総入力
    total_input = inputs + bias
    ## 層の出力
    output = sigmoid(total_input)

    return output

### 隠れ層
## 隠れ層のユニット数
hidden_layer_units = 7
## 隠れ層の出力
hidden_layer_output = forward_propagation(hidden_layer_units, input_layer_units, input_layer_output)

### 出力層
## 出力層のユニット数
output_layer_units = 8
## 出力層の出力
output_layer_output = forward_propagation(output_layer_units, hidden_layer_units, hidden_layer_output)

### 結果を出力
print(output_layer_output)

結果

[0.13505787 0.28972478 0.79229405 0.96599546 0.21776713 0.20493699
 0.49640212 0.16498288]

参考

• [第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)
• 多層パーセプトロンを実装してみよう！【機械学習】
• パーセプトロンとニューラルネットワーク – 知的好奇心
• ニューラルネットワークをわかりやすく解説！
• ベクトルの内積や行列の積を求めるnumpy.dot関数の使い方
• NumPy, randomで様々な種類の乱数の配列を生成 – nkmk note
• 【Python】シグモイド関数 / 複雑な関数定義
• なぜ乱数のシード値は42なのか？
• NumPy配列ndarrayの末尾に要素・行・列を追加するappend | note.nkmk.me